“出分当天，看到朋友和同学陆续发出的成绩单后，我也刷新了查分页面，A-Level数学的A*和AS的三门a出现在了眼前，真是有一种悬着的石头终于落下来的感觉。A-Level成绩对于英国院校的申请来说，至关重要。除了内容的难度，对我们candidates的认真细致也有着不低的要求。我个人觉得，大家想要取得理想的成绩，最重要的就是要在日常的学习阶段中做到脚踏实地，扎实学好每一个知识点，认真对待学校里的每一场mock，提升我们的实力，从而让我们有的信心去拿下a，甚至A*。”上海诺科学校AS年级朱同学如是说道。

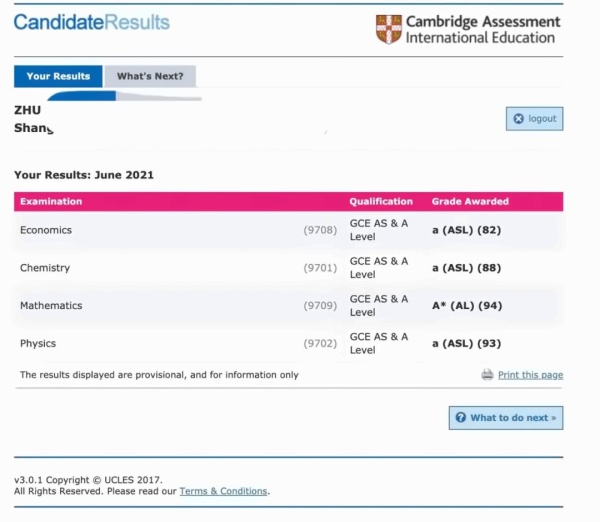
8月10日下午1点，A-Level考试出分啦!诺科AS年级的同学们经过一年的紧张备考，最终取得了满意的成绩。那么，这些高分的背后暗藏着什么样的备考秘诀呢?

学弟学妹们，下面，让我们一起来听听朱学长的各科学习与备考心得吧~

1. A-Level数学，A*

A-Level数学是课程体系中的基础学科，而大家未来的专业，无论是理科还是文科，这门课程都是热门课程。为了能在AS年级的竞赛和后续的大学入学考试(STEP，MAT等)中拿下不错的成绩，我决定在AS年级的时候就要修完四卷的基础数学。在得知我的这个决定以及未来专业方向后，教务处的老师们就帮我设置了单独的数学小班课，以便我在AS年级学完后，直接参加AS+A2数学考试。基础数学可以分为三个部分：纯数学、统计学与力学。其中，纯数学的比重较大，在学习的过程中老师也会将重心放在纯数学上，并根据我的具体学习情况调整学习顺序和计划，最终目标肯定是在考试中拿下A*。普通数学的统计1更偏向于概率分布和计数，压轴题往往会是排列组合，或者正态分布的运用。在这些学习过程和复习阶段中，Colin老师都会根据我的弱项进行针对性的练习，并且帮我总结归纳了技术方法与技巧，并做了一定的内容衍生，对我的帮助很大。

A-Level 数学的难度不高，但知识面广，向量、复数、微积分、微分方程都会涉及，而想要参加竞赛或者高阶数学考试的学弟学妹们，在了解了基础内容后还要做好衍生学习。比如，为什么复数和向量是相邻的章节?是否有什么?棣莫弗公式是否可以将三角函数与复数起来?麦克劳林公式又是如何解释复数可以写成棣莫弗形式与欧拉复数形式的?对于这些内容的拓展学习，学校的每一位数学老师都会很热心和我讨论，并对于课本外的知识做一些解释和延伸。比如，在我的数学学习和STEP备考阶段，Diana老师作为统计学的专家，也会一起帮助我解决相关问题，并辅导我。

2. AS化学，a

在化学的学习过程中，Fei老师的特点就是不追求“快餐式”备考，他更鼓励我们追求知识本身，而这正是A-Level化学学习的关键。当我对化学键的理解还不够准确的时候，他会在课下时间专门找到我，通过图片和模型形象地给我解释化学键的原理。在我一度想要跳过一些章节学习的时候，他会通过化学键和分子结构从而引出分子间的作用力，给我解释了化学课程章节中紧密的。因为他的耐心与用心，我的化学备考有了平稳的进步，并在最后取得了理想的a。

3. AS物理，a

A-Level物理更注重我们对于知识本身的理解。为了帮助我们更好地理解，Dana老师在复习阶段针对每一个章节制作了思维导图，复习讲解每个物理量的定义，每个物理公式的推导步骤，十分清晰。物理是实验基础学科，因此，我们每周都会有实验课。这不仅是让我们练习动手做实验的能力，也很好地帮助我们去探究变量间的关系，以及对于数据的分析与处理。这些过程对于我的备考帮助很大。

4. AS经济，a

经济作为我选择的唯一一门文科课程，说实话，心里还是很不自信的。对于英语相对较弱的我来说，在论文中有条不紊地将所学的经济词条和经济学原理运用于解释一些社会中的经济现象，确实有难度，但也是想要拿到高分的关键。对此，Emily老师在课程学习阶段会对于每一个经济词条做严格的要求，在我懒得去记那么死板的定义时，她会一遍遍地让我回答关于定义格式的问题。事实证明，理解了这些经济学定义后，对我的论文写作会有很大的帮助。在复习阶段，Emily老师也整理了很多笔记资料，让我们归纳总结并且还扩展了一些beyond syllabus的范例，这些知识的确对我们的考试助益良多。

目前，暑假已经过了一半，新的学期即将开始，很多同学马上要进入A-Level年级了。我建议大家，先要掌握好A-Level的知识点，做好备考准备。在学有余力的情况下，与专业相关的学科竞赛也可以多多参加。很多同学问我：“竞赛真的在申请中能起到很大的作用吗?”对于我而言，竞赛是对我A-Level课程外知识学习成果的检测，现在的竞赛更有趣味性，很多题目旨在激发我们对于学科的兴趣，参加竞赛对申请的帮助很难有量化标准，但是在学习竞赛时收获的知识是真真正正存在的。对数学竞赛感兴趣的同学可以从代数、几何、组合、数论等方面起步，例如，代数中的代换思想，几何中的射影变换，组合中的递推与图论对应，数论中的构造思想等。在竞赛的过程中，大家也可以接触到一些高等数学，如，傅立叶变换、线性代数、数学分析等。当大家接触的难题多了，就会发现藏在竞赛题目背后的高等背景。竞赛的用处，不仅限于申请，这些问题的思考角度和深度和队友因为题目争论的经历，才是学习和参加竞赛的意义。

开学在即，祝福大家在新的学年里，好好学习，天天向上!

上海诺科学校报名、校园参观及了解招生动态，请： ，或通过下方报名通道登记。